Conjecture 66. Gaps between consecutive twin pairs

Luis Rodríguez sent the following conjecture:

...I search for a formula that would give the approximate value of the maximum gap between twin primes. I propose  0.45 (Log N)^3 . This produces acceptable numbers. The following is a table of mine: 

GAP         N          0.45 (LOG N)^3
210        5879             294
630       62927             607
1452      851801            1146
1512     2870471            1480
1722     9925709            1882
2256    30754487            2306
2634    78796691            2705

N represents the first prime of the pair of twins where the gap appears.

Let's name the two pairs of consecutive twins this was: {(p1,p1+2; p2,p2+1}. Then, according to Luis, N=p1, Gap=p2-p1, and his conjecture is this one:

Gap ~ k.(ln(p1))³, k ~ 0.45

Q1. Can you justify this Conjecture or suggest a better one?

_____
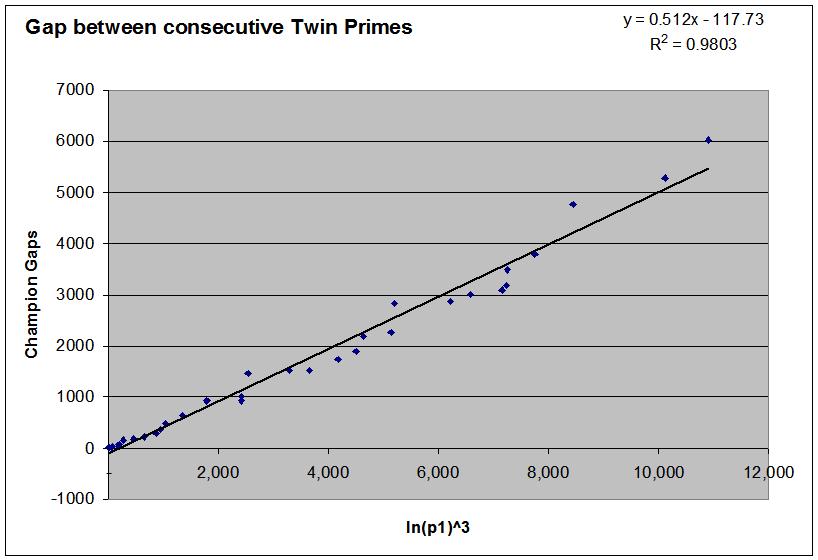
Note: I believe that the formula of Luis is related to the so called "champion gaps" (a gap is a champion when it first occurs and no other gap before is larger than it)

Contribution came from Carlos Rivera

***

Carlos Rivera wrote

Here are my own computations for all the champion gaps less than 6032 (p1<2^32):

and here is the corresponding graph.

***