Conjecture 61. THE MEAN MAXIMUM GAP BETWEEN PRIMES

Luis Rodríguez sent the following conjecture:

p(n)= Prime
p(n+1)= Inmediate superior
Dp=p(n+1)-p(n)
Expected value of gap near p(n)=[Log(Pn)-LogLog(Pn)]^2
Z=Log p(n)

CONJECTURE:
Lim Sup{Dp/(Z - Log Z)^2}=1 when n --> Infinte

Luis sent the following Table on support of his conjecture:

Chi^2 = 15.2. For 23 degrees of liberty that means 90% of level of significance.

QUESTION: Can you design a formula more adjusted than this?
____

Ref. 'The New Book of Prime N. Records' - PAULO RIBENBOIM - Springer  1996
'First ocurrence of prime gaps'    - NICELY & NYMAN  (2005) from: http://www.trnicely.net/gaps/

 

Contributions came from J K Andersen & Jan van Delden

***

J. K. Andersen wrote:

The formulation in conjecture 61
Lim Sup{Dp/(Z - Log Z)^2}=1 when n --> Infinte
is equivalent to Cramér's conjecture (conjecture 7)
Lim Sup{Dp/Z^2}=1 when n --> Infinite

They are equivalent because:
{Dp/Z^2} / {Dp/(Z - Log Z)^2} = (Z - Log Z)^2 / Z^2
= 1 - (2*Log Z)/Z + (Log Z)^2/Z^2 --> 1 when Z --> infinite

The last column in Rodríguez' table only stays so close to 1 because
he writes "To discard" instead of the value 1.1402 for the remarkable
gap of 1132 at 1693182318746371.
That data point is included in the table for Cramér's Conjecture at
http://wvwright.net/
In the definition of Lim Sup, any data point is eventually "discarded".

***

Jan wrote:

The way the problem is posed is not fully specified. I do understand he wants to state a conjecture regarding the maximal gap between primes, in contrary to for instance Cramérs conjecture regarding the average primegap. For instance I presume only those p(n) are allowed for which the corresponding gap d(p(n)) is increasing.

Secondly I'm not sure whether Luis Rodríguez wants to use the lim sup. I get the impression he wants to state something about the fact that a maximum gap is used and hence uses the lim sup. Where, considering his table, an 'ordinary' limit would be more approriate. Which would perhaps be more in line with the name given to the conjecture.

Lastly his Chi^2 calculation/interpretation is not very appropriate. First it can only be applied if the listed (increasing) gaps can be considered independent. If so, the value 15.2 with 23 degrees of freedom, states that the probability that such a Chi-square value is found (or larger) given the values of the maximal gaps in the table is about 90%. Hence the deviation between the found values and the expected values can be considered small (enough), given the large probability of discovering such a deviation. [Another approach could be to construct a confidence interval around 15.2 and check whether the value 0 (no deviation) lies inside this interval].

***

Luis replied to Jan:

My conjecture differ from original Cramer's only in the divisor: (ln p- ln ln p)^2 instead (ln p)^2.
It has been observed that the difference between Cramer and the real maximum gap augment with p .
My curve gives little differences negatives and positives.
The use of Chi^2 is based in the supposition that the true law of max. diff. is (ln p - ln ln p)^2,
then the differences between the gaps and the formula are experimental errors.
The aim in searching a formula was the necessity of a mean for predicting the gap near a large number or
to predict the number in whose neighbourhood a large gap can occur .
Example. The gap 2000 is expected to occur in the neighbourhood of 1.4 x 10^21.
 

***

Jan Feliksiak wrote on April 1,2021:

***
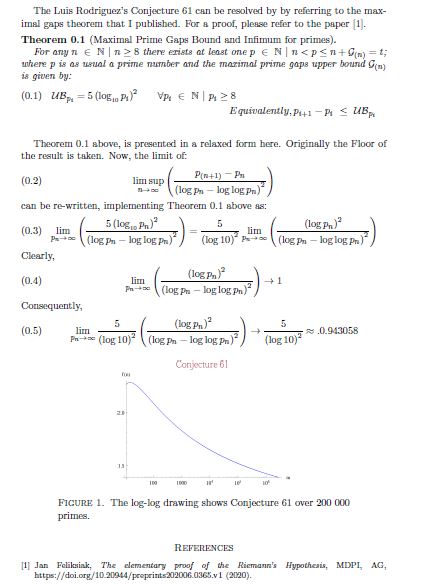