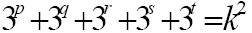
Regarding the above equation, Muneer Jebreel Karama conjectures that:

1) there is no solution if p, q, r, s & t are prime numbers.

On the other hand, he has shown that:

2) if the prime condition is eliminated the same equation has infinite solutions.

Question: Can you verify both claims from Karama?

Contributions came from Patrick Capelle, Rudolph Knjzek, T.D. Noe, Dan Dima & Adam Stinchcombe.

***

Capelle wrote:

***

Knjzek wrote:

Let's start with claim 2)

Let k = 3^(n+1)
k^2 = 9*3^(2n) = (1 + 1 + 1 + 3 + 3)*3^(2n)
k^2 = 3^(2n)+3^(2n)+3^(2n)+3^(2n+1)+3^(2n+1)

There is an infinity of solutions of the form k = 3^(n+1) , p=q=r=2n , s=t=2n+1

This gives us a counterexample to claim 1)

Let's set n=1 and we have k=9, p=q=r=2 and s=t=3 ( 2 and 3 are prime, aren't they?).

3^2 + 3^2 + 3^2 + 3^3 + 3^3 = 9^2

***

T. D. Noe wrote:

As stated, the conjecture is false because {p,q,r,s,t}={2,2,2,3,3} is a solution with k=9. So let's suppose that the primes should be distinct.

It is well known that for all integers k, we have k^2 = 0 (mod 4) or k^2 =
1 (mod 4). So let's look at sums of the form 3^p + 3^q + 3^r + 3^s + 3^t (mod 4). It is easy to see that 3^x = 1 (mod 4) or 3^x = 3 (mod 4) depending on whether x is even or odd, respectively. Hence, modulo 4, the sum of 5 powers of 3 is one of the following:
1+1+1+1+1 = 1 (mod 4) *
3+1+1+1+1 = 3 (mod 4)
3+3+1+1+1 = 1 (mod 4) *
3+3+3+1+1 = 3 (mod 4)
3+3+3+3+1 = 1 (mod 4) *
3+3+3+3+3 = 3 (mod 4)
Only the equations marked with (*) can yield squares because the sum is 1 (mod 4). Those equations have either 5, 3, or 1 even powers of 3, respectively. Because there is only one even prime, only the last marked equation is possible (one even and four odd exponents).

Now let's consider the equation modulo 8. It is well known that for all integers k, we have k^2 (mod 8) equals 0, 1, or 4. Again, it is easy to see that 3^x = 1 (mod 8) or 3^x = 3 (mod 8) depending on whether x is even or odd, respectively. Therefore, modulo 8, the sum of five powers (one even and four odd exponents) of 3 becomes
3+3+3+3+1 = 5 (mod 8). Because this sum is 5, it means that the sum cannot be a square and the conjecture is true for distinct primes.

If the prime condition is eliminated, then {p,q,r,s,t}={2,3,4,5,6} is a solution with k=33. It is easy to see that {p,q,r,s,t}={2+u,3+u,4+u,5+u,6+u} is a solution for any positive even number u. Hence, there are an infinite number of solutions in this case.

***
 

Dan Dima wrote:

3^p + 3^q + 3^r + 3^s + 3^t = k². 

1) If p, q, r, s & t are all prime numbers the only solution is: (3,3,2,2,2) & k=9 since 3³ + 3³ + 3² + 3² + 3² = 9² and the permutations.

Only if p, q, r, s & t are distinct prime numbers the conjecture is true, but generally this is not true so the conjecture is false!

Proof.

Suppose p ³ q ³ r ³ s ³ t ³ 2 all primes. Note that k must be odd and for any odd k² º 1 (mod 8) and 3^k º 3 (mod 8).

1. p = q = r = s = t = 2 Þ 5*3² = k² , contradiction Þ no solution.
2. p > q = r = s = t = 2 Þ 3^p-2 + 4 = m². (k = 3m)

p-2 is odd so 3^p-2 º 3 (mod 8) Þ  m² º 7 (mod 8), contradiction Þ no solution.

      3.   p ³ q > r = s = t = 2 Þ 3^p-2 + 3^q-2 + 3 = m².

p-2, q-2 both odd so 3^p-2 º 3^q-2 º 3 (mod 8) and the equality may hold mod 8:

3^p-3 + 3^q-3 + 1 = 3n² Þ p = q = 3, otherwise by contradiction it cannot hold mod 3.

Hence (3,3,2,2,2) is such a solution.

      4.   p ³ q ³ r > s = t = 2 Þ 3^p-2 + 3^q-2 + 3^r-2 + 2 = m².

p-2, q-2, r-2 odd so m² º 3 (mod 8), contradiction Þ no solution.

5. p ³ q ³ r ³ s > t = 2 Þ 3^p-2 + 3^q-2 + 3^r-2 + 3^s-2 + 1 = m².

m² º 5 (mod 8), contradiction Þ no solution.

6. p ³ q ³ r ³ s ³ t > 2 Þ 3^p-2 + 3^q-2 + 3^r-2 + 3^s-2 + 3^t-2 = m².

m² º 7 (mod 8), contradiction Þ no solution.

Hence if p, q, r, s & t are all prime numbers there is a solution (3,3,2,2,2). More generally this is the only solution if we consider p, q, r, s & t odd numbers or 2.

2) If the prime condition is eliminated one can easily find many different parameterizations to show that it has infinite solutions.

If (p, q, r, s, t, k) is a solution then (p+2, q+2, r+2, s+2, t+2, 3k) is also a solution.

I think it is quite impossible to determine all the solutions for this equation. Some parameterizations are:

(2i+1, 2i+1, 2i, 2i, 2i, 3ⁱ⁺¹)
(2i+3, 2i+2, 2i+2, 2i+1, 2i, 7*3ⁱ)
(2i+2j, 2i+j+1, 2i+j, 2i+1, 2i, 3ⁱ(3^j+2))

***